In EIT problem solving it is necessary to calculate the
derivatives of the measured voltages respect to conductivity.
Complete matrix of partial derivatives is called the Jacobian,
sometimes called the sensitivity matrix and its rows are called
sensitivity maps [1].
Jacobian - the matrix of the sensitivity of the voltage
across the electrodes to the change in electrical conductivity
within the object in the application of different current patterns.
is as follows:
The Jacobian can be computed quite effectively as an
integral of the scalar product of gradients of current and
measurement fields [1]. Measurement fields can be calculated
assuming that the measurement patterns are converted into
current patterns.
The potential
field produced by passing a current
through the current electrodes is:
The potential field produced by passing a current through the measuring electrodes is:
- is the m-th measurement at the d-th current sheet template, then the formula for calculating the
sensitivity matrix is as follows:
Properties of sensitivity matrix (Jacobian) largely determine the
characteristics and behavior of the solution of the EIT.
To investigate the properties of the matrix we use the singular
value decomposition (singular value decomposition, SVD). Singular
value decomposition of the matrix J of size RxK is its representation in
the following form:
where:U is orthogonal matrix of size RxR,
V is orthogonal matrix of size KxK,
is matrix of size RxK.
On the main diagonal of matrix  the singular numbers are contained in descent order and all non-deagonal elements are equal to zero.
the singular numbers are contained in descent order and all non-deagonal elements are equal to zero.
 the singular numbers are contained in descent order and all non-deagonal elements are equal to zero.
the singular numbers are contained in descent order and all non-deagonal elements are equal to zero.
From singular value decomposition we can calculate the Moore-Penrose pseudoinverse matrix:
Condition number of matrix is:
where: - is the largest singular value,
- is the largest singular value,- is the smallest singular value,
- is a norm of matrix.
Singular value decomposition is an important tool for ill-posedness investigation. The plot of the eigenvalues characterizes the instability of the inverse problem (Fig. 1).
 |
| Fig. 1 |
Note the properties of the sensitivity matrix:
1. Jacobian matrix is rank-deficient. This suggests that one or more rows and columns of the matrix are linear combinations of other rows and columns. The linear dependence is showed by a jump in singular values of singular spectrum. As a rule, the smallest singular values equivalent to or less than machine precision.
2. The Jacobian has a large condition number.
3. A relative decline of singular values and Picard coefficients have a special meaning. For ill-posed problems with noisy observations a stable solution exists when a Picard condition is satisfied [2]. According to it, the coefficients
2. The Jacobian has a large condition number.
3. A relative decline of singular values and Picard coefficients have a special meaning. For ill-posed problems with noisy observations a stable solution exists when a Picard condition is satisfied [2]. According to it, the coefficients
should fall to zero faster than the singular values. From (Fig.1) we can see that not all singular numbers should be used to get suitable solution.
Sources:
[1] Polydorides, N. Image
Reconstruction Algorithms for Soft-Field Tomography: Ph.D. thesis / Polydorides — Manchester, United
Kingdom: N. UMIST, 2002. —250 p.
[2] Hansen P. C. Regularization Tools A Matlab Package for Analysis and
Solution of Discrete Ill-Posed Problems / Hansen P. C. —Denmark: Technical University
of Denmark, Department of Mathematical Modeling, 1998. — 111 p.











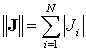

Could you bring me an example please? I have a 4 element mesh, and I can solve the forward problem, but when I tried to calculate the Jacobian, I don't understand well the concept (what is [grad phi I d] * [grad phi I m] numerically?). Thank you for your info.
ReplyDeletesame question as Miguel Angel San Pablo, waiting for your kind reply
ReplyDelete