The Spline is a smooth, piecewise-defined polynomial function. Spline has a high smoothness degree at pieces joining points, which are called knots.
The expansion involves
the integer shifts of the central B-spline of degree  denoted by
denoted by  multiplied by B-spline coefficients
multiplied by B-spline coefficients  .
.
 denoted by
denoted by  multiplied by B-spline coefficients
multiplied by B-spline coefficients  .
.
B-spline
B-spline (Basis spline)
is a symmetrical, compactly supported bell-shaped function. It is constructed
from the  -fold convolution of a
rectangular pulse
-fold convolution of a
rectangular pulse  :
:
 -fold convolution of a
rectangular pulse
-fold convolution of a
rectangular pulse  :
:
In this way spline is characterized
by set of coefficients  . The representation of discrete signal by spline
coefficients introduces splines as powerful instrument for signal processing.
. The representation of discrete signal by spline
coefficients introduces splines as powerful instrument for signal processing.
 . The representation of discrete signal by spline
coefficients introduces splines as powerful instrument for signal processing.
. The representation of discrete signal by spline
coefficients introduces splines as powerful instrument for signal processing.
Take a closer look at B-splines. The generic
representation of B-spline is also described by following equation:
Using such equation it is possible to get
values of any-order B-spline. However the explicit equations for a b-splines of
certain degrees are existed to avoid unnecessary computations:
The B-spline of degree  (cubic B-spline) has a
minimum curvature property and is widely used for performing high-quality
interpolation.
(cubic B-spline) has a
minimum curvature property and is widely used for performing high-quality
interpolation.
 (cubic B-spline) has a
minimum curvature property and is widely used for performing high-quality
interpolation.
(cubic B-spline) has a
minimum curvature property and is widely used for performing high-quality
interpolation.
Java example code
There is Java code which builds and plots
b-splines functions with different degrees. The BSplines class has method
bspline(int degree, double x) where degree is degree of b-spline (0,1,2 and
3) and x is the point in which we want
to get the value of b-spline. The enter point is the main procedure which
created shifted b-splines of different orders and draws them.
package com.blogspot.shulgadim.splines; import java.awt.Color; public class BSplines { public double bspline(int degree, double x){ double betta; double t; betta = 0; if(degree == 0){ if ((x > -0.5) && (x < 0.5)){ betta = 1.0; } else if( Math.abs(x) == 0.5){ betta = 0.5; } else if( Math.abs(x) > 0.5){ betta = 0.0; } } else if( degree == 1){ if ((x<=-1) || (x>=1)){ betta = 0.0; } else if ((x>-1) && (x<0)){ betta = x+1; } else if ((x>0) && (x<1)){ betta = -x+1; } else if( x==0){ betta = 1.0; } } else if (degree == 2 ){ t = 1.5; if ((x <= (0-t)) || (x >= (3-t))){ betta = 0.0; } else if ((x >= (0-t)) && (x< (1-t))) { betta = ((x+t)*(x+t))/2.0; } else if ((x >= (1-t)) && (x< (2-t))) { betta = ((x+t)*(x+t)-3.0*(x-1+t)*(x-1+t))/2.0; } else if ((x >= (2-t)) && (x< (3-t))) { betta = ((x+t)*(x+t) - 3.0*(x-1+t)*(x-1+t) + 3.0*(x-2+t)*(x-2+t))/2.0; } } else if (degree == 3 ){ if ((Math.abs(x)>=0) && (Math.abs(x)< 1)) { betta = 2.0/3.0 - Math.abs(x)*Math.abs(x) + (Math.abs(x)*Math.abs(x)*Math.abs(x))/2.0; } else if ((Math.abs(x)>=1) && (Math.abs(x)< 2)) { betta = ((2-Math.abs(x))*(2-Math.abs(x))* (2-Math.abs(x)))/6.0; } else if (Math.abs(x) >=2) { betta = 0.0; } } return betta; } public static void main(String[] args){ double x[]; double b0[]; double b1[]; double b2[]; double b3[]; int M = 200; x = new double[M]; b0 = new double[M]; b1 = new double[M]; b2 = new double[M]; b3 = new double[M]; for( int k=0; k<x.length; k++){ x[k] = (k-50.0)/30.0; } BSplines bSplines = new BSplines(); for( int k=0; k<x.length; k++){ b0[k]= bSplines.bspline(0,x[k]); b1[k]= bSplines.bspline(1,x[k]-1); b2[k]= bSplines.bspline(2,x[k]-2); b3[k]= bSplines.bspline(3,x[k]-3); } Figure figure = new Figure("bsplines","x","betta"); figure.line(x,b0, Color.BLUE, 2.0f); figure.line(x,b1, Color.RED, 2.0f); figure.line(x,b2, Color.BLACK, 2.0f); figure.line(x,b3, Color.MAGENTA, 2.0f); } }
The Figure class creates the figure on which the functions are plotted. It suports ordinary line and stem styles of function plot representations.
package com.blogspot.shulgadim.splines; import java.awt.*; import javax.swing.*; import org.jfree.chart.*; import org.jfree.chart.axis.*; import org.jfree.chart.plot.*; import org.jfree.chart.renderer.xy.*; import org.jfree.data.xy.*; public class Figure { private JFrame frame; private XYPlot plot; private int dataSetsCounter = 0; public Figure(String name, String xName, String yName) { frame = new JFrame("Figure"); frame.getContentPane().setLayout(new BorderLayout()); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); plot = new XYPlot(); plot.setBackgroundPaint(Color.WHITE); plot.setDomainGridlinePaint(Color.LIGHT_GRAY); plot.setRangeGridlinePaint(Color.LIGHT_GRAY); NumberAxis domainAxis = new NumberAxis(xName); ValueAxis rangeAxis = new NumberAxis(yName); plot.setDomainAxis(domainAxis); plot.setRangeAxis(rangeAxis); JFreeChart chart = new JFreeChart(plot); RenderingHints renderingHints = new RenderingHints(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON); renderingHints.put(RenderingHints.KEY_STROKE_CONTROL, RenderingHints.VALUE_STROKE_PURE); chart.setRenderingHints(renderingHints); chart.removeLegend(); chart.setTitle(name); ChartPanel chartPanel = new ChartPanel(chart); frame.getContentPane().add(chartPanel, BorderLayout.CENTER); frame.setSize(400, 400); frame.setVisible(true); } public void line(double x[], double y[], Color color, float lineWidth) { XYDataset dataset = createDataset(x,y); plot.setDataset(dataSetsCounter, dataset); XYLineAndShapeRenderer renderer = new XYLineAndShapeRenderer(true, false); BasicStroke basicStroke = new BasicStroke(lineWidth); renderer.setSeriesStroke(0, basicStroke); renderer.setSeriesPaint(0, color); plot.setRenderer(dataSetsCounter, renderer); dataSetsCounter++; } public void stem(double x[], double y[], Color color, float lineWidth) { XYDataset dataset = createDataset(x,y); plot.setDataset(dataSetsCounter, dataset); XYBarRenderer renderer = new XYBarRenderer(0.98f); renderer.setShadowVisible(false); renderer.setSeriesPaint(0, color); plot.setRenderer(dataSetsCounter, renderer); dataSetsCounter++; } private XYDataset createDataset(double x[], double y[]) { XYSeries series = new XYSeries(""); for(int i=0; i<y.length;i++){ series.add(x[i],y[i]); } XYSeriesCollection dataset = new XYSeriesCollection(); dataset.addSeries(series); return dataset; } }
 |
| The figure representing B-splines of degrees 0,1,2 and 3 |
Sources:
[1] M. Unser “Splines: A Perfect Fit for Signal and Image Processing” IEEE Signal Processing Magazine, vol. 16, no. 6, pp. 22-38, November 1999.




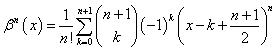



Great step by step solution, thanks for the help! http://wisentechnologies.com/it-courses/java-training.aspx" title="Java Training in Chennai">Java Training in Chennai. | http://wisenitsolutions.com/IT-Courses/Java-Training" title="Java Online Training India">Java Online Training India | http://wisenitsolutions.com/IT-Courses/JavaEE-Training" title="Java EE Online Training" >Java EE Online Training
ReplyDelete