
How to solve systems of linear differential equations? Here we describe three ways: Runge - Kutta method, and two similar ways to each other using the method of state space.
Let our process is described by the following differential equation:
This equation can be written as:
where:
1 Method: solution by the method of numerical integration (Runge - Kutta method)
x0 = [1
1];
tspan = 0:0.1:10;
[T,x1] = ode45(@odefun,tspan,x0);
figure;
subplot(2,1,1);plot(T,x(:,1));title('x1')
subplot(2,1,2);plot(T,x(:,2));title('x2')
Differ. equation is written in a function and stored in a separate file called odefun.m:
function [dx] = odefun(t,x)
dx = zeros(2,1);
A = [-1 0
0 0.5];
dx = A*x;
 |
| The solution of equation (x1 and x2) |
2 Method: solving equation using the state space method
1. Differentiating consistently equation (*) : in a Taylor series around the point
in a Taylor series around the point  :
:4. Series before
 is:
is:
then
The are two ways to implement the algorithm:
1 way:
x0 = [1
1];
tspan = 0:0.1:10;
A = [-1 0
0 0.5];
x = zeros(2,length(tspan));
for i = 1:length(tspan)
t = tspan(i);
F = expm(A*t);
x(:,i) = F*x0;
T(i) = tspan(i);
end
x = x';
figure;
subplot(2,1,1);plot(T,x(:,1));title('x1')
subplot(2,1,2);plot(T,x(:,2));title('x2')
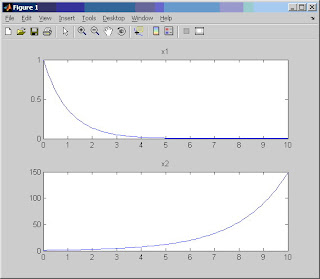 |
| The solution of equation (x1 and x2) |
2 way:
x0 = [1
1];
tspan = 0:0.1:10;
dt = tspan(2) - tspan(1);
A = [-1 0
0 0.5];
x(:,1) = x0';
F = expm(A*dt);
for i = 2:length(tspan)
x(:,i) = F*x(:,i-1);
T(i) = tspan(i);
end
x = x';
figure;
subplot(2,1,1);plot(T,x(:,1));title('x1')
subplot(2,1,2);plot(T,x(:,2));title('x2')
 |
| The solution of equation (x1 and x2) |











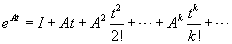

Thank You. It was very interesting.
ReplyDeleteI wonder, is there any way to solve this problem with other programming language, rather then Matlab?
ReplyDeleteYou can use any programming language to solve this problem... It's just example was made for Matlab.
Delete